Return of the Kinnari

มีข่าวดีที่รอคอยมานานจากเนคเทค คือตอนนี้ ฟอนต์แห่งชาติ ทั้งสามฟอนต์ภายใต้สัญญาอนุญาต GPL ได้ เปิดดาวน์โหลด แล้ว

ซึ่งหมายความว่า โครงการ ThaiFonts-Scalable จะสามารถแก้ไขแจกจ่ายฟอนต์แห่งชาติได้ครบทั้งสามฟอนต์แล้ว โดยได้ฟอนต์กินรี (ฟช ๑) ที่ขาดหายไปกลับมาเพิ่ม

ขอขอบคุณทุกท่านที่เนคเทคที่มีส่วนช่วยดำเนินการครับ โดยเฉพาะ คุณกำธร และ พี่ปลา

ช่วงนี้ ใน CVS ของ ThaiFonts-Scalable กำลังปรับ GSUB, GPOS ของฟอนต์ต่าง ๆ เพื่อให้สนับสนุนแพลตฟอร์มต่าง ๆ มากขึ้น หลังจากปรับเรื่องนี้เสร็จแล้ว สิ่งที่จะแทรกก็คือการเพิ่มฟอนต์กินรีละครับ

มีความคืบหน้าเล็กน้อยที่น่าจะเล่า คือหลังจากที่ผมปล่อย ThaiFonts-Arundina 0.1.1 และ file ITP ใน Debian ก็ปรากฏมีผู้พบเห็นและแจ้งไปที่โครงการ DejaVu ว่าควรจะเอาไปรวมกับ DejaVu เลยไหม ซึ่งผลการพิจารณาขั้นแรกที่ดูที่ตัว Sans ก่อน เขาบอกว่า Arundina ตัวอักษรไทยเส้นบางกว่าอักษรอังกฤษมากเกินไป ผมก็เลยส่งผู้เข้าประกวดหมายเลข 2 (ซึ่งอันที่จริงผมอยากส่งเข้าไปพร้อมกัน แต่ครั้งนี้ผมไม่ได้เป็นคนส่งเอง เพราะบังเอิญ Arundina ถูกแมวมองจับตัวไปส่งเสียก่อน) คือ Waree ของคุณ วิทยา ที่อยู่ในชุด ThaiFonts-Scalable ซึ่งเบื้องต้นเขาบอกว่า Waree เข้ากันได้เนียนเปี๊ยบกับ DejaVu Sans เลย แต่ติเรื่องความสูงว่ามันสูงไม่เท่าตัวฝาหรั่ง ไหน ๆ เว็บโครงการฟอนต์แห่งชาติก็มี Fontbook ซึ่งเป็น spec สำหรับสร้างฟอนต์ไทยมาให้ด้วย ผมเลยหอบเปิดไปอ้างกับเขาซะ ว่าฟอนต์ไทยเขาดีไซน์กันแบบนี้ ผลจะเป็นอย่างไรต้องติดตามกันต่อไปครับ

Dragon and Lion Dance Invitation Tournament 2007

พร้อม ๆ กับซีเกมส์ที่โคราช เมื่อ 13-14 ธ.ค. ที่ผ่านมา มีการแข่งขันกีฬามังกรสิงโตนานาชาติ เฉลิมพระเกียรติ ๘๐ พรรษา ที่จังหวัดขอนแก่น

การแข่งขันมีนักกีฬาจาก 7 ประเทศ/เขตการปกครองเข้าแข่งขัน คือ สาธารณรัฐประชาชนจีน, ไต้หวัน, ฮ่องกง, มาเลเซีย, สิงคโปร์, อินโดนีเซีย และไทย จัดการแข่งขันทั้งหมด 4 ประเภท คือสิงโตค่ายกล, มังกรเก้าเซียน back light (กลางคืน), สิงโตตอดอกเหมย และมังกรเก้าเซียนกลางวัน

มีกีฬานานาชาติที่บ้านทั้งที เลยตามไปเก็บรูปไว้ สถานที่แข่งขันคือลานหน้าศาลหลักเมืองขอนแก่นที่เพิ่งสร้างขึ้นแทนที่ศาลหลักเมืองเดิม ถือว่าได้มังกรและสิงโตมาร่วมสมโภชศาลหลักเมืองใหม่ไปในตัว จะมีก็แต่มังกรกลางคืนที่ต้องการความมืด จึงไปแข่งที่สนามกีฬาในร่มของจังหวัด

กีฬามังกรสิงโต 2007

ผลการแข่งขันครั้งนี้ มาเลเซียซึ่งเป็นเจ้ากีฬานี้กวาดรางวัลไปตามระเบียบ:

ประเภท	ชนะเลิศ	รองชนะเลิศอันดับ 1	รองชนะเลิศอันดับ 2
สิงโตค่ายกล	มาเลเซีย	ฮ่องกง	ไทย
มังกรกลางคืน	มาเลเซีย	ฮ่องกง	ไต้หวัน
สิงโตตอดอกเหมย	มาเลเซีย	ไทย	อินโดนีเซีย
มังกรกลางวัน	ไทย	สิงคโปร์	มาเลเซีย

ทีมไทย ส่งประเภทละ 2-3 ทีม โดยมีทีมจากชมรมกีฬาสิงโต-มังกร กังปัก และทีมจากชมรมลูกเจ้าพ่อหลักเมืองขอนแก่น ที่ได้รางวัลเป็นทีมจากลูกเจ้าพ่อหลักเมืองขอนแก่นทั้งหมด

รูปแบบการแข่งขัน เขาให้คะแนนกันเหมือนยิมนาสติกเลยละ มีกรรมการจาก 7 ชาตินั่งแยกกันให้คะแนน แล้วก็มีกรรมการกลางคอยรวมคะแนน และให้คะแนนภาพรวมด้วย ดูมีกติกาและมาตรฐานดีพอสมควร ยินข่าวว่าจะได้บรรจุใน Asian Indoor Games เร็ว ๆ นี้ด้วย

ในบรรดาการแข่งขันประเภทต่าง ๆ มังกรกลางคืนนับเป็นสิ่งที่แปลกตาที่สุด ยังไม่เคยเห็นมาก่อน และทำให้ได้รู้ว่า การแห่มังกรสิงโต ตอนนี้กลายเป็นกีฬาที่มีกฎกติกาอย่างเป็นทางการเรียบร้อยแล้ว แต่ละชาติก็พยายามพัฒนามาตรฐานของตัวเองอย่างเอาจริงเอาจัง

Cubic vs Quadratic Splines

ระหว่างทำฟอนต์ Arundina รวมทั้งฟอนต์ Waree เองที่ผ่านไป เจอประเด็นหนึ่งให้ตัดสินใจ ระหว่างการใช้ cubic spline กับ quadratic spline เป็นรูปแบบสำหรับการ edit ฟอนต์ ว่าจะใช้รูปแบบไหนดี เนื่องจากต้นฉบับเขาใช้ quadratic แต่ผมคุ้นเคยกับ cubic

จากการทดลอง และคิดถึงหลักเหตุผลจากทฤษฎีเบื้องหลัง ก็ทำให้ตัดสินใจในที่สุดกับฟอนต์ดังกล่าว แต่ก่อนจะไปถึงคำตอบ ขอเท้าความสักนิด บันทึกความคิดเกี่ยวกับเรื่องนี้ก่อน

โมเดลของเส้นโค้งที่นิยมใช้กันมากที่สุดในแวดวงคอมพิวเตอร์กราฟิกส์ ก็คือ Bézier curve โดยแทนเส้นโค้งด้วยสมการ parametric เป็นพหุนาม ซึ่งสามารถเป็น linear, quadratic, cubic หรือดีกรีเท่าไรก็ได้ เส้นโค้งดีกรี n จะอาศัยจุดควบคุมทั้งหมด n + 1 จุด โดยเป็นจุดปลาย 2 จุด และจุดควบคุมเส้นโค้งอีก n - 1 จุด กล่าวคือ

ดีกรี 1 เป็นเส้นตรง สมการแทนเส้นตรงจากจุดปลาย P₀ ไป P₁ คือ

B(t) = (1 - t)P₀ + tP₁ ; 0 ≤ t ≤ 1

ดีกรี 2 (quadratic) สมการแทนเส้นโค้งจากจุดปลาย P₀ ไป P₂ โดยมีจุดควบคุมเส้นโค้ง P₁ คือ

B(t) = (1 - t)²P₀ + 2(1 - t)tP₁ + t²P₂ ; 0 ≤ t ≤ 1

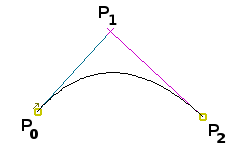
ดีกรี 3 (cubic) สมการแทนเส้นโค้งจากจุดปลาย P₀ ไป P₃ โดยมีจุดควบคุมเส้นโค้ง P₁ และ P₂ คือ

B(t) = (1 - t)³P₀ + 3(1 - t)²tP₁ + 3(1 - t)t²P₂ + t³P₃ ; 0 ≤ t ≤ 1

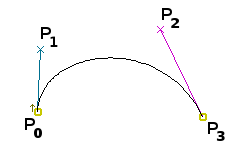
ที่นิยมใช้มีแค่นี้ เนื่องจากดีกรีที่สูงกว่านี้จะจัดการยาก โดยที่นิยมใช้มากที่สุดคือ cubic Bézier curve เนื่องจากความอิสระของจุดควบคุมกำลังเหมาะกับการปรับแก้ด้วยมือ โปรแกรมกราฟิกส์ทั่วไปก็มักใช้ cubic Bézier นี้ จนกระทั่งเมื่อพูดถึง Bézier curve ลอย ๆ ก็จะหมายถึง cubic Bézier โดยปริยาย

Postscript ก็ใช้ cubic Bézier แทนเส้นโค้ง ฟอนต์ Postscript จึงแทนโค้งของตัวอักษรด้วย cubic Bézier ส่วนฟอนต์แบบ TrueType จะใช้ quadratic Bézier

แล้วข้อดีข้อเสียของเส้นโค้งทั้งสองแบบนี้เป็นยังไง?

การแปลงรูปแบบ

ถ้ายังไม่พูดถึงการแก้ไข การเก็บเส้นโค้งในรูป quadratic จะสามารถแปลงเป็น cubic ได้โดยไม่เสียความละเอียด เนื่องจากเส้นโค้งที่ดีกรีสูงกว่าสามารถลดรูปลงมาเป็นดีกรีที่ต่ำกว่าได้ ในขณะที่การแปลงจาก cubic เป็น quadratic จะไม่สามารถแทนเส้นโค้ง cubic ด้วย quadratic แบบแม่นยำได้ จะต้องมีการ interpolate จุดควบคุมระหว่างกลางเพิ่มเติม

เกี่ยวกับการลดรูปนี้ คุณสามารถพิสูจน์จากสมการ parametric ได้ว่า สำหรับเส้นโค้ง quadratic ที่มีจุดควบคุม P₀, P₁ และ P₂ สามารถแทนได้ด้วยเส้นโค้ง cubic ที่สมมูลกันโดยมีจุดควบคุม P₀, (P₀/3 + 2P₁/3), (2P₁/3 + P₂/3), และ P₂

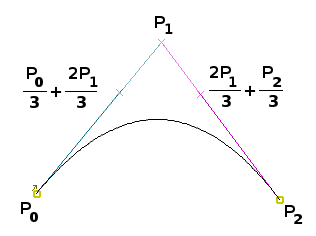
จำนวนจุดควบคุม

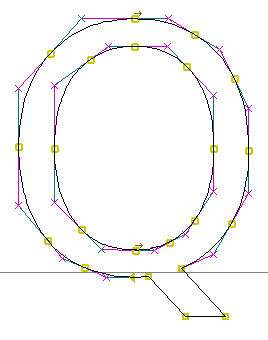
ความที่โค้ง quadratic มีจุดควบคุมโค้งเพียงจุดเดียว ความเป็นอิสระของโค้งจึงต่ำ การแทนโค้งใหญ่ ๆ จึงต้องอาศัยจำนวนโค้งย่อยมาต่อกันจำนวนมากกว่าโค้ง cubic ดังนั้น จุดต่อโค้งของโค้ง quadratic โดยทั่วไปจึงมากกว่าโค้ง cubic

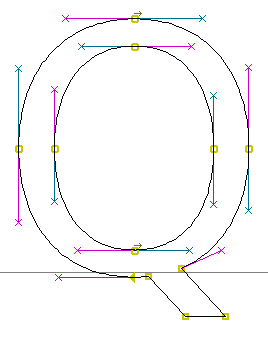จำนวนจุดในโค้ง quadratic	จำนวนจุดในโค้ง cubic

การแก้ไข

เมื่อนำเส้นโค้งมาต่อกันเป็นโค้งใหญ่ แต่ละจุดเชื่อมต่อก็จะมีเวกเตอร์ควบคุมสองเส้น โดยชี้ไปยังจุดควบคุมของเส้นโค้งก่อนหน้าเส้นหนึ่ง กับชี้ไปยังเส้นโค้งส่วนถัดไปอีกเส้นหนึ่ง ซึ่งจุดเชื่อมต่อนี้ มีได้สามรูปแบบ คือ

• จุดหักมุม (corner point) เป็นจุดที่เส้นโค้งมีการหักมุม เวกเตอร์ควบคุมทั้งสองด้านจะเอียงทำมุมอย่างอิสระ ไม่ขึ้นต่อกัน
• จุดสัมผัสโค้ง (tangent point) เป็นจุดที่เปลี่ยนจากเส้นตรงเป็นเส้นโค้ง หรือเส้นโค้งเป็นเส้นตรง โดยมีความต่อเนื่องของเส้นต่อไป เวกเตอร์ควบคุมด้านที่ชี้ไปยังส่วนเส้นโค้งจะทำมุมเท่ากับมุมของส่วนเส้นตรง ส่วนเวกเตอร์ควบคุมที่ชี้ไปยังส่วนเส้นตรงนั้นไม่มี คือเป็นเวกเตอร์ศูนย์
• จุดต่อโค้ง (curve point) เป็นจุดเปลี่ยนจากโค้งหนึ่งเป็นอีกโค้งหนึ่ง โดยมีความต่อเนื่องของเส้น เวกเตอร์ควบคุมทั้งสองด้านจะทำมุมเท่ากัน แต่ชี้ในทิศตรงกันข้าม

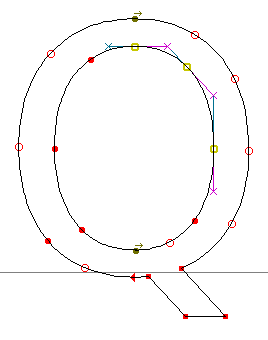
จุดสองประเภทแรกนั้น ไม่ค่อยมีปัญหาเท่าไรกับการแก้ไข ไม่ว่าจะเป็น quadratic หรือ cubic แต่จุดต่อโค้งนั้น จะทำให้แก้ไขลำบากถ้าเป็น quadratic เนื่องจากเส้นโค้ง quadratic มีจุดควบคุมเพียงจุดเดียว ซึ่งจะมีผลกับเส้นโค้งทั้งสองปลาย แล้วเมื่อเวกเตอร์ควบคุมของส่วนของเส้นโค้งสองเส้นมาผูกติดกันด้วยมุมเอียง การปรับจุดควบคุมของโค้งหนึ่ง จึงกระทบถึงอีกโค้งหนึ่งทั้งโค้งอย่างเลี่ยงไม่ได้

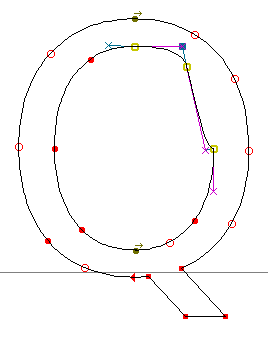การแก้ quadratic curve: ก่อน	การแก้ quadratic curve: หลัง

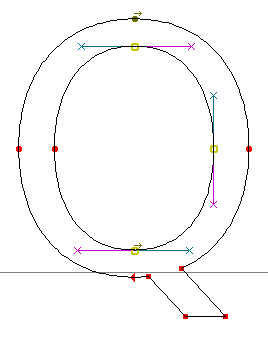
ในขณะที่โค้ง cubic จะเป็นอิสระกว่า เพราะมีจุดควบคุมสองจุด การปรับจุดควบคุมของโค้งหนึ่ง จึงมีผลต่อส่วนของเส้นโค้งที่แก้ไขอยู่เท่านั้น ไม่ใช่ไปกระทบต่อโค้งถัดไปด้วย

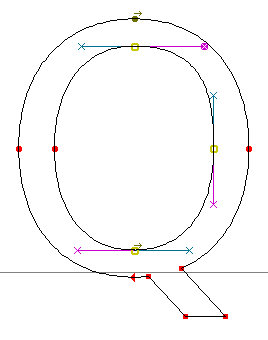การแก้ cubic curve: ก่อน	การแก้ cubic curve: หลัง

เมื่อประกอบเข้ากับเงื่อนไขที่ว่า โค้ง quadratic มีจำนวนจุดต่อมากกว่า ซึ่งหมายถึงจุดต่อโค้งอยู่ใกล้กันมาก ผลของความกระทบกระเทือนจึงมีอัตราสูงกว่าด้วย ทำให้การแก้ไขโค้ง quadratic ยิ่งยากขึ้นไปอีก

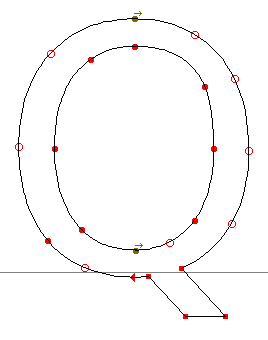
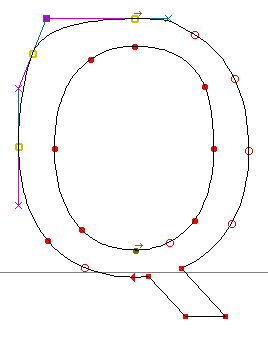
fontforge มีมาตรการคลายความอึดอัดตรงนี้บ้าง ด้วยการกำหนดให้จุดต่อโค้งบางจุดเป็น interpolated คือให้คำนวณตำแหน่งจากจุดข้างเคียง แทนที่จะให้แก้ไขโดยตรง การปรับจุดข้างเคียง ก็จะมีผลต่อตำแหน่งของจุดนี้ด้วย ทำให้ดูเสมือนไม่มีจุดต่อโค้งนี้อยู่ แต่สิ่งที่ได้คือ จุดควบคุมโค้งที่อยู่ถัดจากจุดนี้ไป จะเป็นอิสระจากการปรับโค้ง เสมือนหนึ่งกำลังปรับโค้งใหญ่ที่มีจุดควบคุมสองจุด นับเป็นวิธีที่ชาญฉลาดทีเดียว

การแก้ quadratic curve ที่มี interpolated point: ก่อน	การแก้ quadratic curve ที่มี interpolated point: หลัง

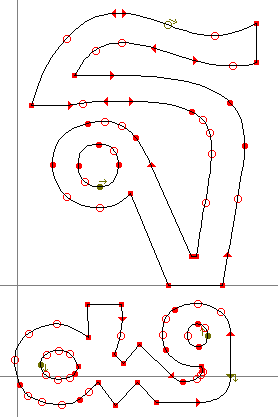
อย่างไรก็ดี จำนวนจุดต่อโค้งที่มากเกินไปของโค้ง quadratic ก็ยังทำให้การปรับเส้นโค้งเป็นไปอย่างทุลักทุเล โดยเฉพาะสำหรับ glyph ที่มีโค้งซับซ้อน เพราะต้องปรับโค้งย่อยทีละส่วน แทนที่จะปรับโค้งโดยรวมได้กว้างเหมือนโค้ง cubic

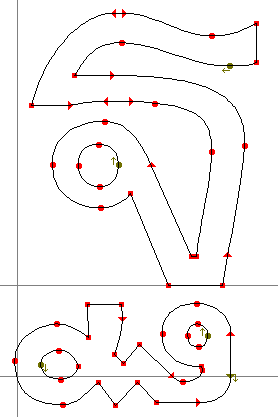ตัวอย่าง glyph ที่ซับซ้อนเมื่อเป็น quadratic	ตัวอย่าง glyph ที่ซับซ้อนเมื่อเป็น cubic

สรุป

• โดยปกติ การสร้างฟอนต์ในรูปโค้ง cubic แล้วให้โปรแกรมแปลงเป็น TrueType ที่เป็น quadratic จะทำให้ปรับแก้ฟอนต์ได้ง่ายกว่า แม้การแปลงเป็น quadratic จะต้องมีการ interpolate เพิ่ม แต่ก็ถือว่าโปรแกรมส่วนใหญ่ interpolate แบบอัตโนมัติได้ดี
• ถ้าต้องปรับแต่งฟอนต์ที่ต้นแบบเป็น TrueType ซึ่งใช้โค้ง quadratic ก็อาจจะขึ้นอยู่กับว่า ต้องปรับแก้ spline ของ glyph ต่าง ๆ หรือเปล่า ถ้าไม่ต้องปรับ การเก็บเป็น quadratic ก็ย่อมรักษาข้อมูลเดิมของฟอนต์ได้ครบถ้วน แต่ถ้าจำเป็นต้องปรับ การแปลงเป็น cubic โดย simplify spline เพื่อลดจำนวนจุดต่อโค้งด้วย จะทำให้ทำงานสะดวกกว่า ใช้เครื่องมือต่าง ๆ ได้ครบครันกว่า แม้จะเสียข้อมูลบางส่วนไป แต่การ interpolate ของโปรแกรมสร้างฟอนต์ก็ถือว่าไม่ทำให้เสียรูปเส้นโค้งเดิมไปเท่าไรนัก เทียบกับการปรับโค้งที่เป็นระเบียบกว่าแล้ว ถือว่าคุ้มค่า

ยาวหน่อยครับ blog นี้ ถือว่าเป็นการเรียบเรียงความคิดตัวเองไปในตัว

ThaiFonts-Scalable 0.4.8

หลังจากตกแต่ง + รอฟอนต์กินรีอยู่นาน ในที่สุด thaifonts-scalable 0.4.8 ก็ ออกแล้ว โดยการเปลี่ยนแปลงที่สำคัญคือ มีฟอนต์ใหม่ 2 ฟอนต์ (Sawasdee และ Waree), TrueType hint และการสังเคราะห์ฟอนต์ Browallia

สิ่งที่พลาดหรือตกไปในรุ่นนี้คือ

• การ hack เพื่อสนับสนุน MacOS และโปรแกรมของ Adobe ตามที่เคยกล่าวถึงในท้าย blog เก่า เนื่องจากจาก การทดสอบ พบว่าระบบเหล่านั้นไม่สนับสนุน GPOS สำหรับภาษาไทยเอาเสียเลย จำเป็นต้องย้อนกลับไปใช้ ligature rule แบบดิบ ๆ ซึ่งอาจตีกับ GSUB rule เดิมที่มีอยู่ ถ้าจะพยายามทำให้ได้ ก็จะกลายเป็นการถอยหลังมากเกินไป น่าจะพยายามผลักดันให้ระบบเหล่านั้นสนับสนุนภาษาไทยให้เต็มที่มากกว่า (ล่าสุด จากการทดสอบ Leopard ดู ดูเหมือนเริ่มสนับสนุน OpenType ภาษาไทยแล้ว แต่ยังมีปัญหานิดหน่อย)
• ฟอนต์กินรี ที่ทางเนคเทคกำลังช่วยจัดการเรื่อง license ให้อยู่ แต่ผมมีกำหนดการหนึ่งที่พยายามทำให้ทัน คือ กำหนดการของ Hardy ซึ่งมีกำหนด DebianImportantFreeze วันที่ 13 ธ.ค. นี้ จึงควรพยายาม upload แพกเกจใหม่เข้าใน Debian อย่างน้อยระลอกหนึ่งก่อน เพื่อให้ฟอนต์ได้เข้า Hardy โดยอัตโนมัติ หากพ้นกำหนดนี้ไปแล้ว โอกาสเข้า Hardy ก็ยังมีอยู่ และหากฟอนต์กินรีจัดการเสร็จก่อน Hardy จะ freeze จริง ๆ ก็ยังมีโอกาสได้เข้า เพียงแต่ต้องมีการ request แบบ manual

ตอนนี้ build deb เรียบร้อยแล้วครับ รอคำตอบจาก sponsor อยู่

ขั้นต่อไปคือ ทำฟอนต์ Arundina ให้เรียบร้อย ก่อนส่งเข้า Debian ต่อไป

Update นิดหนึ่งสำหรับเพื่อนฝูงที่ถามไถ่อาการผม อาทิตย์ที่ผ่านมา ต้องเข้ากรุงเทพฯ แต่ลืมเอาน้ำตาเทียมไปด้วย พอต้องนั่งรถเมล์-เดินถนนในกรุง ก็เลยกำเริบหนัก ใครบางคนช่วยแนะนำให้ผมถือโอกาสไปตรวจที่โรงพยาบาลจักษุโดยเฉพาะ คราวนี้ได้ตรวจละเอียดกว่าเดิม โดยหมอวัดปริมาณน้ำตาแล้ว ผมมีน้ำตาแห้งกว่าคนปกติมาก โดยซึมในกระดาษที่วัดเพียง 3 มม. ในขณะที่คนปกติจะซึม 10 มม. หมอก็เลยสั่งให้หยอดน้ำตาเทียมให้ถี่ขึ้น ใช้แว่นกันลมทุกครั้งที่ออกข้างนอก โดยเฉพาะหน้าหนาวที่อากาศแห้ง ก็ยิ่งต้องระวังเป็นพิเศษ หากยังไม่ดีขึ้น อาจต้องรักษาด้วยการอุดท่อระบายน้ำตา

สรุปว่าต้องพักสายตาจากหน้าจอให้มากขึ้นครับ งานอาจจะเดินช้าหน่อย แต่เพื่อให้ทำงานได้ในระยะยาวก็ต้องยอม