Fine-tuning Quadratic Splines in Fontforge
นับจากที่ได้เพิ่ม layer ผสมใน Fonts-TLWG เพื่อแก้ปัญหาเรื่อง build reproducibility ในรุ่น 0.7.0 ก็ได้เปิดช่องทางสำหรับการ fine-tune quadratric spline ของฟอนต์ TrueType เพียงแต่ผมยังไม่ได้ทำกับ Fonts-TLWG ในทันที เพราะได้กลับไปทำ layer ผสมกับ Fonts-Arundina เสียก่อน และได้ถือโอกาสทดลอง fine-tune quadratic spline ต่อด้วย
หลังจากที่เพิ่ม layer ผสมกับทุกฟอนต์ในชุด Arundina แล้ว ก็ได้ทดลอง fine-tune quadratic spline ต่อ ซึ่งก็ทำเสร็จแค่ Arundina Sans เท่านั้น พอมาทำ Arundina Sans Mono ต่อ ปรากฏว่าเกิดเหตุ Fontforge ตายกลางคันขณะ save ทำให้ข้อมูลที่แก้ไขมาได้ครึ่งทางแล้วสูญหายทั้งหมด แม้แต่กระบวนการ recovery ของ Fontforge เองก็กู้ข้อมูลขึ้นมาไม่ได้! ถ้าจะเริ่มใหม่ก็ต้อง check out ฉบับที่ยังไม่ปรับเส้นจาก git ออกมาทำใหม่นั่นแหละ
เป็นอุทาหรณ์ว่าควร commit git ให้บ่อยกว่านี้ ถึงยังไม่เสร็จก็ควร commit ไว้ก่อน แล้วค่อยใช้ option
ในครั้งต่อ ๆ ไปก็ยังได้!--amend
ก็เลยตัดสินใจหยุดทำ Arundina ไว้แค่นั้น แล้วเตรียมตัดออกรุ่นใหม่เสียก่อน โดยขอบันทึกสิ่งที่ได้เรียนรู้จากการปรับเส้นฟอนต์ Arundina ไว้ ณ ที่นี้ก่อน ก่อนที่จะนำไปใช้กับ Fonts-TLWG ต่อไป
ปรับ Quadratic และ Cubic Spline ไปด้วยกัน
ในระยะแรกนั้น ผมปรับเฉพาะ quadratic layer เข้าหา cubic layer โดยพยายามให้ curve ทาบกับ cubic layer ได้สนิทด้วยจำนวนจุดที่พอเหมาะ โดยตัดจุดที่ไม่จำเป็นออก และเติมจุดบางจุดที่เห็นว่าน่าจะเป็นประโยชน์ต่อการ hint แต่เมื่อได้ปรับไปเรื่อย ๆ ก็ได้พบกรณีที่ต้องปรับ cubic layer ควบคู่กันมากขึ้นเรื่อย ๆ จนในที่สุดผมก็ปรับทั้งสอง layer ควบคู่กัน ซึ่งปรากฏว่าคุณสมบัติของโค้งทั้งสองแบบได้เสริมกันและกันในการจัด control point ต่าง ๆ ได้เป็นอย่างดี
การปรับทั้งสอง layer ควบคู่กันยังมีข้อดีอีกอย่าง คือเราสามารถลดปริมาณงานในอนาคตหากมีการ copy ข้ามจาก cubic layer มายัง quadratic layer อีกด้วย เพราะจะได้จำนวนจุด quadratic ที่เหมาะสมทันที ไม่ต้องมานั่งปรับใหม่ รวมถึงกรณีที่ต้องการ generate ฟอนต์ TrueType ด้วยการแปลงจาก cubic layer กลางอากาศ (อย่างที่เราเคยทำในสมัยก่อน)
หรือแม้กระทั่งสำหรับการ generate ฟอนต์ PostScript หรือฟอนต์ OpenType ที่ใช้ cubic spline เอง ก็จะได้โค้งที่ได้สมมาตรสวยงาม และยังอาจช่วยให้ rasterize ได้เร็วขึ้นสำหรับบาง engine ได้อีกด้วย (เช่น สำหรับ rasterizer ที่ render Bézier curve ด้วยการแบ่งครึ่ง curve แบบ recursive บนพื้นฐานของ De Casteljau’s algorithm)
ส่วนวิธีการปรับนั้นจะกล่าวถึงต่อไปเป็นลำดับ
Quadratic Spline ใน Fontforge
จากที่ผมเคยเขียนเปรียบเทียบ quadratic และ cubic spline ไว้เมื่อนานมาแล้ว ทั้งในแง่คณิตศาสตร์ การแปลงระหว่างกัน จำนวนจุดที่ใช้แทนโค้ง และการแก้ไข โดยในส่วนของการแก้ไขนั้น ผมได้กล่าวไว้ว่าโค้ง quadratic แก้ไขยากกว่า เพราะการแก้ไขแต่ละจุดจะกระทบถึงจุดข้างเคียงเสมอ แต่ Fontforge มีสิ่งที่ช่วยคลายความอึดอัดตรงนี้ ด้วยจุดต่อโค้งชนิด interpolated ที่ตำแหน่งของจุดต่อโค้งจะคำนวณจากจุดควบคุมข้างเคียง ทำให้ลดการกระทบกระทั่งลงได้
จุด interpolated ในที่นี้ขอเรียกว่า จุดกะ
ในโค้ง quadratic เป็นจุดต่อโค้ง (curve point) ที่อยู่กึ่งกลางระหว่างจุดควบคุมสองจุด และในทางกลับกัน จุดต่อโค้งที่มีแขนสองข้างยาวเท่ากันก็จะถือเป็นจุดชนิด interpolated โดยอัตโนมัติใน Fontforge เช่นกัน (ยกเว้นจุดที่ผู้ใช้กำหนดให้ห้าม interpolate)
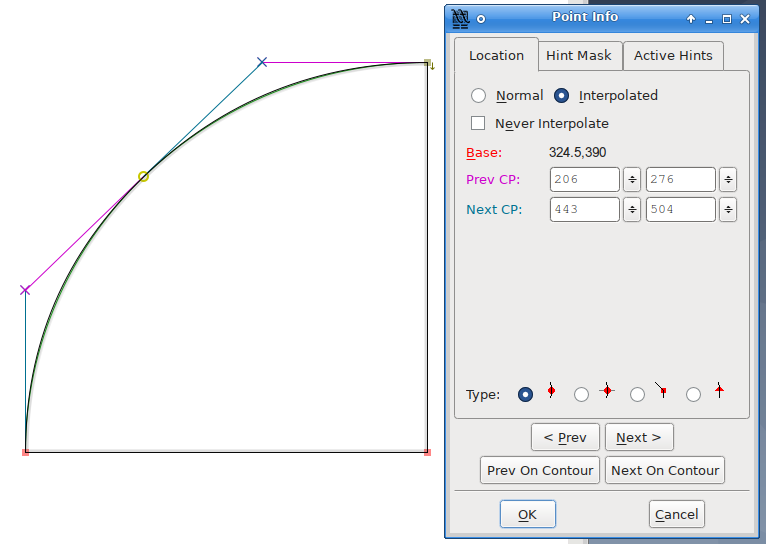
ความพิเศษของจุดกะนี้ก็คือ การแก้ไขจุดควบคุมข้างหนึ่งจะไม่ส่งผลกระทบถึงจุดควบคุมอีกข้างหนึ่ง เพียงแต่จะทำให้ตำแหน่งของจุดกะเองเปลี่ยนไปเป็นจุดกึ่งกลางใหม่ ซึ่งทำให้เกิดผลคล้ายกับการแก้ไข cubic spline โดยไม่ต้องสนใจการมีอยู่ของจุดกะ
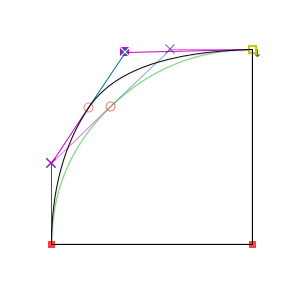
การประมาณ Cubic Curve ด้วย Quadratic Curve
ดังที่ได้กล่าวไว้ใน blog เดิม ว่าการแปลง quadratic curve เป็น cubic จะเป็นการแปลงแบบแม่นตรง แต่ในทางกลับกัน คือจาก cubic curve เป็น quadratic จะเป็นการประมาณเท่านั้น เนื่องจาก quadratic curve มีความเป็นอิสระ (degree of freedom) น้อยกว่า ดังนั้น เมื่อคุณคัดลอก spline จาก cubic layer มา quadratic layer จึงมีการประมาณค่าเกิดขึ้น
มีอัลกอริทึมจำนวนหนึ่งสำหรับประมาณ cubic curve ด้วย quadratic เช่น แบ่ง curve เป็นส่วนย่อย ๆ ที่เมื่อตัดสัมประสิทธิ์ดีกรีสามออกแล้วได้ quadratic curve ที่ใกล้เคียงพอ (มี paper ที่คล้ายกัน), แบ่งครึ่ง curve ที่ t=0.5 แล้ว solve หาจุดควบคุม quadratic curve ที่ใกล้เคียงของทั้งสองส่วน ฯลฯ
สำหรับ Fontforge แล้ว ใช้การประมาณด้วยจุดกะ โดยอยู่บนพื้นฐานของทฤษฎีซึ่งพบจากการทดลองแต่ยังไม่มีข้อพิสูจน์ทางคณิตศาสตร์ว่า ถ้าแบ่ง cubic curve เป็นช่วง ๆ ด้วย parameter ที่ห่างเท่า ๆ กันแล้ว ปรากฏว่าจุดแบ่งเหล่านั้นจะอยู่กึ่งกลางระหว่างจุดควบคุมข้างเคียงพอดี ซึ่งหมายความว่าสามารถแทนจุดแบ่งทุกจุดด้วยจุดกะได้ ด้วยทฤษฎีนี้ Fontforge จึงประมาณ cubic spline ด้วย quadratic spline ที่เติมจุดกะตามแนวเส้นโค้งเสมอ
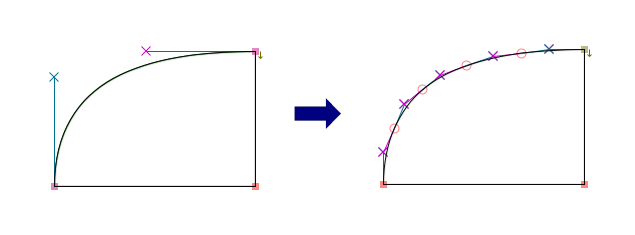
Fontforge จะพยายามประมาณโค้งโดยเติมจุดกะให้น้อยที่สุด ยิ่งไม่ต้องเติมจุดกะเลยยิ่งดี แต่หากยังคลาดเคลื่อนมากก็ลองเติมหนึ่งจุด สองจุด สามจุด ไปเรื่อย ๆ จนกว่าความคลาดเคลื่อนจะอยู่ในขอบเขตที่กำหนด
การลดจำนวนจุดกะใน Quadratic Curve
การประมาณของ Fontforge คือการประมาณในทางคณิตศาสตร์ที่มีความแม่นยำสูง แต่ในทาง design แล้ว เราอาจยอมรับความคลาดเคลื่อนได้บ้างโดยไม่ทำให้รูปตัวอักษรเพี้ยนไปจากเดิม ซึ่งแน่นอนว่าเรื่องการผ่อนผันที่ต้องใช้วิจารณญาณอย่างนี้ Fontforge จะไม่สู่รู้ตัดสินใจให้ เราจึงต้องปรับเองด้วยมือ
จากภาพในตัวอย่างข้างต้น มีการเติมจุดกะระหว่างกลาง 4 จุดใน quadratic curve แต่เราสามารถลดจำนวนจุดกะนี้ลงได้ ไม่ว่าจะเพื่อความเรียบง่าย เพื่อลดขนาดข้อมูล (ซึ่งสำคัญสำหรับ web font) หรือเพื่อประสิทธิภาพในการ hint และการ rasterize ก็ตาม โดยแนวทางการลดจุดกะที่เป็นไปได้คือ:
- ตัดจุดกะด้วยมือ โดยเลือกจุดกะที่ต้องการตัดแล้วสั่ง Merge (Ctrl-M)
- ปรับ cubic curve ต้นทางด้วยมือให้สามารถประมาณได้ด้วยจำนวนจุดที่น้อยลง
ทั้งสองวิธีจะได้ quadratic curve ที่คลาดเคลื่อนจาก cubic curve เดิมเล็กน้อย แต่วิธีที่สองจะทำให้ได้ spline สองแบบที่ทาบกันสนิทกว่าแบบแรก เพราะมันถูกปรับไปด้วยกัน
ในฟอนต์ตัวแรก ๆ ที่ทำ ผมใช้วิธีแรก แต่ต่อมาก็ค่อย ๆ เกิดความคิดว่าวิธีที่สองน่าจะเหมาะกว่า และในที่สุดก็เลือกวิธีที่สองเป็นหลัก
แล้ว cubic curve แบบไหนที่จะใช้จำนวนจุดกะน้อยลง?
ก่อนอื่น คนที่เคย edit cubic curve จะรู้ว่าเราสามารถปรับแขนทั้งสองของโค้งได้โดยยังได้โค้งที่ใกล้เคียงกับโค้งเดิม ด้วยการเพิ่มความยาวของแขนข้างหนึ่ง และลดความยาวของแขนอีกข้างหนึ่ง
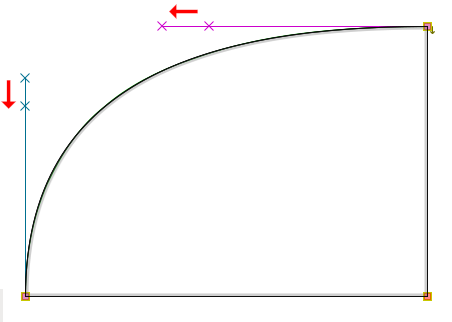
แน่นอนว่าในทางคณิตศาสตร์แล้ว โค้งที่ปรับแล้วถือว่าไม่ใช่โค้งเดียวกับโค้งเดิม แต่ความคลาดเคลื่อนระหว่างโค้งทั้งสองยังอยู่ในขอบเขตที่ยอมรับได้ด้วยสายตามนุษย์ โดยเฉพาะถ้าปรับไม่มาก แต่ถ้าปรับมากเกินไปก็จะเริ่มสังเกตเห็นความแตกต่างเมื่อนำมาทาบกัน (ซึ่งในทาง design เราก็อาจจะยังยอมรับได้อยู่ดี)
สำหรับโค้งในตัวอย่างข้างต้น เมื่อปรับแล้ว copy ข้ามมา quadratic layer เรากลับได้ curve ที่ใช้จุดกะเพียงจุดเดียว จากเดิมที่ใช้ถึง 4 จุด
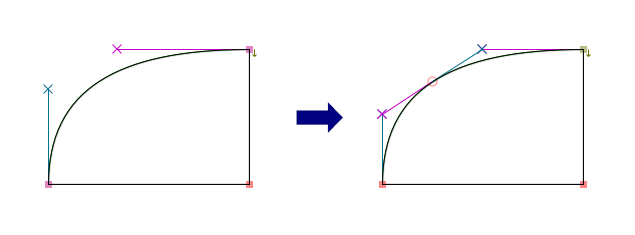
ถามว่า cubic curve แบบไหนที่ใช้จุดกะน้อย? แรก ๆ ที่ลองผิดลองถูกน้ัน ผมอาศัย sense เป็นหลัก คือพยายามให้แขนทั้งสองข้างได้ดุลกัน แต่เมื่อทำไปก็เริ่มถามตัวเองถึงคุณสมบัติทางคณิตศาสตร์ที่ชัดเจนกว่าการใช้ sense ซึ่งในที่สุดก็ได้คำตอบที่กลับไปหาพื้นฐานทางคณิตศาสตร์ของ cubic และ quadratic curve นั่นเอง
จาก blog เดิม ผมได้กล่าวไว้ว่า quadratic curve ที่มีจุดควบคุม P0, P1 และ P2 สามารถแทนได้ด้วย cubic curve ที่สมมูลกันโดยมีจุดควบคุม P0, (P0/3 + 2P1/3), (2P1/3 + P2/3), และ P2
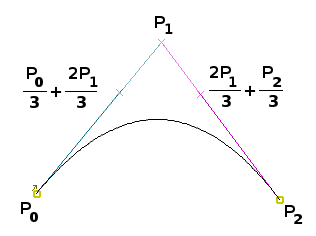
เราสามารถพูดในทางกลับกันได้ว่า cubic curve ที่ว่านี้ เมื่อแปลงเป็น quadratic curve ก็จะใช้จุดควบคุม P0, P1 และ P2 ได้ทันทีโดยไม่ต้องเติมจุดกะ
ถือเป็นอุดมคติของการประมาณโค้ง ยิ่งเราปรับ cubic curve ให้เข้าใกล้อุดมคตินี้มากเท่าไร เมื่อแปลงเป็น quadratic ก็จะใช้จุดกะระหว่างกลางน้อยลงเท่านั้น
อุดมคติที่ว่านี้ มีคุณสมบัติที่เห็นได้จากเรขาคณิตก็คือ เส้นตรงที่เชื่อมระหว่างจุดควบคุมทั้งสองขนานกันกับเส้นตรงที่เชื่อมระหว่างจุดปลายทั้งสอง โดยถ้าความยาวของแขนควบคุมเท่ากับ 2/3 ของระยะไปยังจุดตัดของแขนควบคุมทั้งสองพอดี ก็จะไม่ต้องใช้จุดกะเพิ่มเลย แต่ถ้าไม่ใช่ก็ต้องมีจุดกะเพิ่ม
ฉะนั้น แนวทางโดยทั่วไปก็คือ พยายามเล็งให้ polygon ที่เชื่อมระหว่างจุดปลายและจุดควบคุมของ cubic curve กลายเป็นสี่เหลี่ยมคางหมูหรือใกล้เคียง ซึ่งโดยทั่วไปก็จะทำให้มีจุดกะเพิ่มไม่เกิน 1 จุด
การปรับอื่น ๆ
ในบางกรณี ก่อนที่จะได้ cubic curve ที่สามารถแทนด้วย quadratic curve ที่เติมจุดกะไม่เกิน 1 จุด ก็อาจจำเป็นต้องปรับจุดต่อโค้งต่าง ๆ เพิ่มตามจำเป็น เช่น
- เติมจุดบิดโค้ง (inflection point) เพื่อแบ่งโค้งที่บิดเป็นรูปตัว S ออกเป็นสองส่วน เนื่องจาก quadratic curve ไม่สามารถบิดเป็นตัว S ได้เหมือน cubic curve
- เติมจุดต่อโค้งในโค้งที่หักเลี้ยวไม่สมมาตร จนจำเป็นต้องเติมจุดกะมากกว่า 1 จุด เช่น ในฟอนต์ตัวเอียงที่โค้งเดิมกำหนดจุดต่อโค้งที่ extrema เท่านั้น
การเติมจุดเหล่านี้ หากพิจารณาเฉพาะฟอนต์ที่ใช้ cubic spline อาจดูไม่จำเป็น แต่การเติมจุดต่อโค้งนอกจากจะช่วยให้ใช้จุดกะน้อยเมื่อแปลงเป็น quadratic แล้ว ก็ยังมีผลดีต่อการควบคุมความหนาของเส้นหมึกสำหรับ cubic spline เองด้วย เช่น การมีจุดกำกับที่จุดบิดโค้งก็ย่อมเพิ่มโอกาสการ hint หรือตรึงตำแหน่งที่จุดบิดโค้ง แทนที่จะปล่อยให้โค้งลอยไปมาตามผลการขยับจุดปลายระหว่าง apply hint
แผนการต่อไป
ในฟอนต์ชุด Arundina ที่กำลังจะตัดออกรุ่นนี้ ผมได้ปรับ spline เฉพาะฟอนต์ Arundina Sans เท่านั้น โดยใช้วิธีแรก (ยุบจุดกะใน quadratic spline เท่านั้น) และ commit ไปแล้ว ส่วน Arundina Sans Mono ผมเริ่มใช้วิธีที่สอง แต่น่าเสียดายที่ข้อมูลสูญหายไปหมด จึงไม่ได้รวมมาในรุ่นใหม่นี้ แต่จะนำหลักการที่ได้นี้ไปใช้ปรับฟอนต์ชุด Fonts-TLWG ในลำดับต่อไป
ป้ายกำกับ: fonts-arundina, thaifonts-scalable, typography
