Red-Black Trees

Red-black tree เป็น self-balancing binary search tree ที่ใช้ในโครงการต่างๆ มากมาย เช่น ใน C++ STL, ใน symbol table ของ compiler/interpreter ต่างๆ และใน Linux kernel ด้วยข้อได้เปรียบ AVL tree เรื่องการเพิ่มข้อมูลเพื่อการ balance ในแต่ละโหนดเพียงบิตเดียว ในขณะที่ AVL tree ต้องการอย่างน้อย 2 บิต รวมถึงการ insert และ delete ที่เร็วกว่า แม้จะใช้เวลา search มากกว่าสักหน่อย แต่ก็ยังเป็น O(log n) เหมือนกัน

ฟังดูน่าศึกษาใช่ไหมล่ะ? แต่พอลองค้นดูจริงๆ มันยุ่งกว่าที่คิดมาก

red-black tree เสนอโดย Leonidas J. Guibas และ Robert Sedgewick (PDF) โดยต่อยอดมาจาก symmetric binary B-tree ของ Rudolf Bayer

symmetric binary B-Tree เป็นการสร้าง perfectly-balanced 2-3-4 tree (B-tree ที่มีทางแยกไม่เกิน 4 และทุก leaf มีความลึกเท่ากันหมด) ด้วย binary tree แบบพิเศษ โดยแทนโหนด B-tree ที่มีทางแยก 3 และ 4 ทางด้วย binary node 2 และ 3 โหนดที่เชื่อมกันด้วยลิงก์แนวนอน (เรียกว่า ρ-arc) ส่วนลิงก์ที่เชื่อมระหว่างโหนดของ B-tree ก็เป็นลิงก์แนวตั้ง (เรียกว่า δ-arc)

Guibas และ Sedgewick ได้นำ symmetric binary B-tree มาสร้างคำอธิบายแบบใหม่ โดยให้ทุกลิงก์เป็นลิงก์แนวตั้งทั้งหมด และเรียก ρ-arc ของ Bayer ว่า red link และเรียก δ-arc ว่า black link แล้วเรียบเรียงนิยามและอัลกอริทึมต่างๆ เสียใหม่ กลายเป็น red-black tree

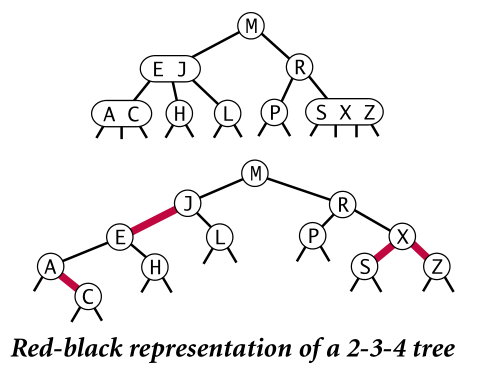
(ภาพจาก Left-leaning Red-Black Trees โดย Robert Sedgewick)

ส่วนเหตุผลว่าทำไมต้องเป็นสองสีนี้ Sedgewick ตอบไว้ในตอนท้ายของการบรรยายครั้งหนึ่งว่า เป็นเพราะขณะที่พัฒนาเรื่องนี้กันที่ Xerox PARC นั้น เริ่มมีการสร้าง laser printer ที่สามารถพิมพ์สีได้ และสีที่พิมพ์ออกมาดูดีที่สุดในขณะนั้นคือสีแดง

อัลกอริทึมสำหรับ insert ของ red-black tree ค่อนข้างจะเทียบเคียงกับของ 2-3-4 tree ได้อย่างตรงไปตรงมา และใช้ operation พื้นฐานในการ rebalance คล้ายกับของ AVL tree แต่อัลกอริทึมสำหรับ delete นั้น Guibas และ Sedgewick บรรยายไว้ไม่ยาวมาก และยังดูมีขั้นตอนเกินจำเป็น โดยมีการ rebalance ทั้งขาลงและขาขึ้น

หลายตำราจึงคิดโครงสร้างของตัวเองขึ้นมาเพื่อปรับปรุงการ delete ซึ่งหลายกรณีส่งผลถึงวิธีอธิบายโครงสร้างทั้งหมดที่ไม่เชื่อมโยงกับ 2-3-4 tree อีกต่อไป เช่น เรียก red/black node แทน red/black link และอธิบายโครงสร้างในเทอมของ parent/sibling/uncle node ไปเลย ซึ่งทำให้จำเป็นต้องมี parent pointer และไม่อาศัย recursion และพอมาถึงเรื่องการ delete หลายตำราก็อธิบายได้น่าปวดหัวมาก บางฉบับถึงกับจั่วหัวไว้ก่อนเลยว่า You will hate it! บางฉบับข้ามเรื่อง delete ไปเสียดื้อๆ เลยด้วยซ้ำ

Red-black tree ที่ใช้ red/black node
(ภาพจาก Wikipedia)

หลังจากอ่านมาหลายแหล่ง รวมถึงฉบับที่ Sedgewick กลับมาเองด้วยโครงสร้าง Left-leaning red-black tree (slide, Coursera) พร้อมกับโค้ดสุด simple แต่ก็มีปัญหาเรื่องการ delete ที่ช้ากว่าของตำราอื่น ดังบทวิจารณ์ Left-Leaning Red-Black Trees Considered Harmful

แต่สุดท้ายก็เจอคำอธิบายที่ผมคิดว่าลงตัวที่สุดจากคอร์สหนึ่งของมหาวิทยาลัย Purdue ซึ่งอธิบาย Red-black tree แบบไม่มี leaning โดยอิง 2-3-4 tree ตั้งแต่ต้นจนจบ อ่านได้ตามลำดับเลยครับ:

1. (2,4) Trees
2. 2-3-4 Trees and Red-Black Trees
3. Deletion from Red-Black Trees